平面几何相关定理

前言

初中的平面几何相关定理，在高中数学中使用的频度还是比较高的。所以别以为三选一变成了二选一，就不需要复习回顾平面几何相关定理了，相反如果熟悉这些内容，反倒对莘莘学子是非常有裨益的。

五大公设

欧几里德的《几何原本》提到的共设，其实就是我们后边所说的公理。

• 公设1：任意一点到另外任意一点可以画直线。

• 公设2：一条有限线段可以继续延长。

• 公设3：以任意点为心及任意的距离可以画圆。

• 公设4：凡直角都彼此相等。

• 公设5：同平面内一条直线和另外两条直线相交，若在某一侧的两个内角和小于二直角的和，则这二直线经无限延长后在这一侧相交。

相关定理

• 1、角平分线性质定理

①.角平分线可以得到两个相等的角。

②.角平分线上的点到角两边的距离相等。

③.三角形的三条角平分线交于一点，称作三角形内心。三角形的内心到三角形三边的距离相等。

④.三角形一个角的平分线，这个角平分线分对边所成的两条线段与这个角的两邻边对应成比例。

• [内角平分线定理，别称：内分比定理，斯霍腾定理]三角形一个角的平分线与其对边所成的两条线段与这个角的两边对应成比例。

已知：如图所示，\(AD\)是\(\Delta ABC\)的内角\(A\)的角平分线，交\(BC\)于点\(D\)。

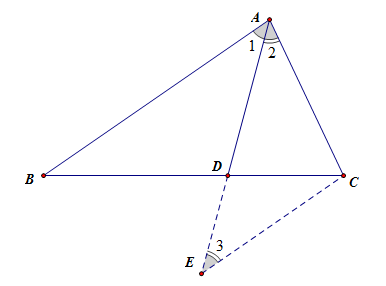
求证：\(\cfrac{AB}{AC}=\cfrac{BD}{DC}\)

证明：过点\(C\)作直线\(CE//AB\)，并且交\(AD\)的延长线于点\(E\)，

则可知\(\Delta ADB\sim \Delta EDC\)，且有\(\cfrac{AB}{EC}=\cfrac{BD}{CD}①\)；

又由\(AB//CE\)可知，\(\angle 1=\angle 3\)，

又已知\(\angle 1=\angle 2\)，故\(\angle 2=\angle 3\)，

即\(CE=AC\)，代入①式可得\(\cfrac{AB}{AC}=\cfrac{BD}{DC}\)。

• 2、全等三角形判定定理：

①SSS（Side-Side-Side）（边边边）：三边对应相等的三角形是全等三角形。

②SAS（Side-Angle-Side）（边角边）：两边及其夹角对应相等的三角形是全等三角形。

③ASA（Angle-Side-Angle）（角边角）：两角及其夹边对应相等的三角形全等。

④AAS（Angle-Angle-Side）（角角边）：两角及其一角的对边对应相等的三角形全等。

下列两种方法不能验证为全等三角形：

AAA（Angle-Angle-Angle）（角角角）：三角相等，不能证全等，但能证相似三角形。

SSA（Side-Side-Angle）（边边角）：其中一角相等，且非夹角的两边相等。

性质定理：对应边相等，对应角相等；

• 3、相似三角形

相似三角形：对应角相等，对应边成比例的两个三角形叫做相似三角形。（similar triangles）。互为相似形的三角形叫做相似三角形。

相似三角形的判定方法：根据相似图形的特征来判断。[对应边成比例，对应角相等]

①.平行于三角形一边的直线和其他两边(或两边的延长线)相交，所构成的三角形与原三角形相似这是相似三角形判定的引理，是以下判定方法证明的基础。这个引理的证明方法需要平行线分线段成比例定理的证明\(\quad\)；

②.如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似；

③.如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似；

④.如果两个三角形的三组对应边的比相等,那么这两个三角形相似；

• 绝对相似三角形[相似形包含全等形]

1.两个全等的三角形一定相似。

2.两个等腰直角三角形一定相似。

3.两个等边三角形一定相似。

• 直角三角形相似判定定理

1.斜边与一条直角边对应成比例的两直角三角形相似。

2.直角三角形被斜边上的高分成的两个直角三角形与原直角三角形相似，并且分成的两个直角三角形也相似。

求证：直角三角形被斜边上的高分成的两个直角三角形与原直角三角形相似，并且分成的两个直角三角形也相似。

证明：由于\(\angle DBA=\angle CAD\)，\(\angle BAD=\angle ACD\)，故\(\triangle BAD\sim \triangle ACD\)①，

由于\(\angle DBA=\angle DBA\)，\(\angle BAD=\angle ACD\)，故\(\triangle BAC\sim \triangle BDA\)②，

由于\(\angle CDA=\angle CDA\)，\(\angle CAD=\angle DBA\)，，故\(\triangle CAD\sim \triangle CBA\)③，

故由①能得到\(\cfrac{BA}{AC}=\cfrac{AD}{CD}=\cfrac{BD}{AD}\)；即\(AD^2=BD\cdot DC\)；

由②能得到\(\cfrac{BA}{BD}=\cfrac{AC}{DA}=\cfrac{BC}{BA}\)；即\(AB^2=BD\cdot BC\)；

由③能得到\(\cfrac{CA}{CB}=\cfrac{AD}{BA}=\cfrac{CD}{CA}\)；即\(AC^2=CD\cdot CB\)；

• 三角形相似的判定定理的推论

  推论一：顶角或底角相等的两个等腰三角形相似。

  推论二：腰和底对应成比例的两个等腰三角形相似。

  推论三：有一个锐角相等的两个直角三角形相似。

  推论四：直角三角形被斜边上的高分成的两个直角三角形和原三角形都相似。

  推论五：如果一个三角形的两边和其中一边上的中线与另一个三角形的对应部分成比例，那么这两个三角形相似。

  推论六：如果一个三角形的两边和第三边上的中线与另一个三角形的对应部分成比例，那么这两个三角形相似。

• 相似三角形的性质

1.相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比。

2.相似三角形周长的比等于相似比。

3.相似三角形面积的比等于相似比的平方。

• 相似三角形的特例

能够完全重合的两个三角形叫做全等三角形。（congruent triangles）

全等三角形是相似三角形的特例。全等三角形的特征：形状完全相同，相似比是\(k=1\)。

全等三角形一定是相似三角形，而相似三角形不一定是全等三角形。

因此，相似三角形包括全等三角形。

• 4、平行线分线段成比例定理[平行截割定理]

等分线段定理：如果一组平行线在一条直线上截得的线段相等,那么在任一条(与这组平行相交的)直线上截得的线段也相等.

平行截割定理【线束定理】：两条直线与一组平行线相交,它们被这组平行线截得的对应线段成比例.

【平行线分线段成比例定理的证明】如图所示，三条直线\(l_1//l_2//l_3\)，三条平行线与直线\(m\)分别相交于点\(A\)、\(B\)、\(C\)，与直线\(n\)分别相交于点\(D\)、\(E\)、\(F\)，则 \(\cfrac{AB}{BC}=\cfrac{DE}{EF}\) .

证明：连结\(AE\)、\(BD\)、\(BF\)、\(CE\)，根据平行线性质[等高]可得[利用等面积法]，\(S_{\triangle ABE}=S_{\triangle DBE}\)，\(S_{\triangle BEC}=S_{\triangle BEF}\)，

则有 \(\cfrac{S_{\triangle ABE}}{S_{\triangle DBE}}=\cfrac{S_{\triangle BEC}}{S_{\triangle BEF}}\)，即\(\cfrac{S_{\triangle ABE}}{S_{\triangle BEC}}=\cfrac{S_{\triangle DBE}}{S_{\triangle BEF}}\)，

根据等高三角形[\(\triangle ABE\)和\(\triangle BCE\)从顶点\(E\)所作的高线相同]的面积比等于底边的比，可得

\[\cfrac{AB}{BC}=\cfrac{DE}{EF} \]

引申，由更比性质、等比性质可得，$$\cfrac{AB}{DE}=\cfrac{BC}{EF}=\cfrac{AB+BC}{DE+EF}=\cfrac{AC}{DF}$$

平行截割定理的推论：平行于三角形一边的直线截其他两边(或者两边的延长线)，截得的三角形与原三角形的对应边成比例.

平行截割定理推论的逆定理：如果一条直线截三角形的两边(或者两边的延长线)所得的对应线段成比例，那么这条直线平行于三角形的第三边。

• 5、直角三角形射影定理，又称“欧几里德定理”，

直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项，每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。

证明：由于\(\angle DBA=\angle CAD\)，\(\angle BAD=\angle ACD\)，故\(\triangle BAD\sim \triangle ACD\)①，

由于\(\angle DBA=\angle DBA\)，\(\angle BAD=\angle ACD\)，故\(\triangle BAC\sim \triangle BDA\)②，

由于\(\angle CDA=\angle CDA\)，\(\angle CAD=\angle DBA\)，，故\(\triangle CAD\sim \triangle CBA\)③，

故由①能得到\(\cfrac{BA}{AC}=\cfrac{AD}{CD}=\cfrac{BD}{AD}\)；即\(AD^2=BD\cdot DC\)；

由②能得到\(\cfrac{BA}{BD}=\cfrac{AC}{DA}=\cfrac{BC}{BA}\)；即\(AB^2=BD\cdot BC\)；

由③能得到\(\cfrac{CA}{CB}=\cfrac{AD}{BA}=\cfrac{CD}{CA}\)；即\(AC^2=CD\cdot CB\)；

• 6、圆周角定理

圆周角的度数等于它所对弧上的圆心角度数的一半\(\angle AOB=2\angle ACB\)，利用三角形的外角定理即可证明，由\(OB=OC\)，可得\(\angle OBC=\angle OCB\)\(\quad\)。

圆心角定理：圆心角的度数等于它所对的弧的度数；

定理推论:

①.一条弧所对的圆周角等于它所对的圆心角的一半；

②.圆周角的度数等于它所对的弧度数的一半；

③.在同圆或等圆中，同弧或等弧所对的圆周角相等；相等的圆周角所对的弧也相等。

④.半圆(直径)所对的圆周角是直角。

⑤.\(90^{\circ}\)的圆周角所对的弦是直径。

注意：在圆中，同一条弦所对的圆周角有无数个。

• 7、圆的切线判定定理和性质定理

判定定理：过半径外端且与这条半径垂直的直线是圆的切线。

性质定理：圆的切线垂直于经过切点的半径。

• 8、相交弦定理

圆内的两条相交弦，被交点分成的两条线段长的积相等。（经过圆内一点引两条弦，各弦被这点所分成的两段的积相等）

证明：如图所示，\(\angle DBA=\angle DCA\)，\(\angle BAC=\angle BDC\)，[同弧所对的圆周角相等]

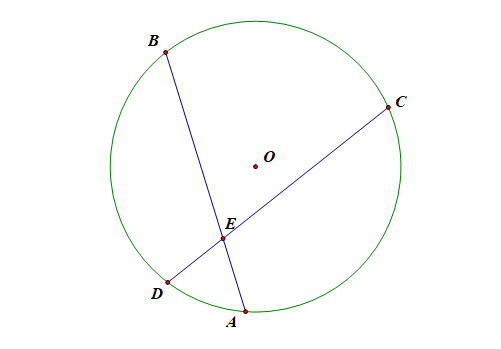
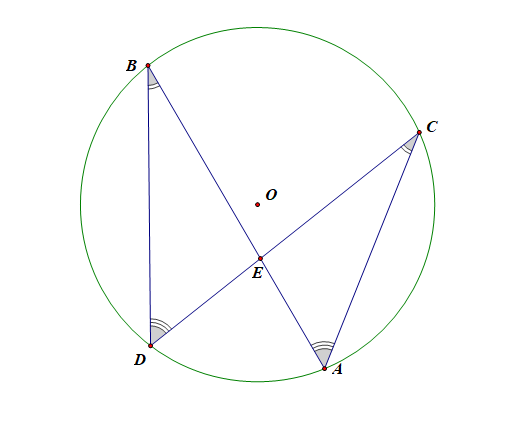
故\(\triangle BED\sim \triangle CEA\)，

故有\(\cfrac{BE}{CE}=\cfrac{ED}{EA}\)，即\(AE\cdot BE=CE\cdot DE\)，

特殊化，当两条相交弦互相垂直，且其中一条弦\(DC\)特殊化为直径\(DC\)时，由垂径定理垂直于弦\(AB\)的直径\(DC\)平分弦\(AB\)，且平分这条弦所对的两条弧，即\(\overset{\frown}{AC}\)\(=\)\(\overset{\frown}{BC}\)，\(\overset{\frown}{AD}\)\(=\)\(\overset{\frown}{BD}\)。\(\quad\)可知，\(DC\perp AB\)，且\(AE=BE\)，此时相交弦定理变形为\(BE^2=DE\cdot CE\)，此时也就和直角三角形射影定理建立了关联。

• 9、圆内接四边形的判定定理与性质定理

判定定理：如果一个四边形的对角互补，那么这个四边形的四个顶点共圆证明思路1： 把被证共圆的四个点连成共底边的两个三角形，且两三角形都在这底边的同侧，若能证明其顶角相等，从而即可肯定这四点共圆。
思路2：把被证共圆的四点连成四边形，若能证明其对角互补或能证明其一个外角等于其邻补角的内对角时，即可肯定这四点共圆。
思路3：反证法；\(\quad\)；

圆内接四边形的判定定理证明：

已知：四边形\(ABCD\)，\(\angle A+\angle C=180^{\circ}\)，

求证：\(A\)，\(B\)，\(C\)，\(D\)四点共圆；

证明：用反证法，由于点\(A\)，\(B\)，\(C\)三点不共线，故由这三个点能唯一的确定一个圆，记为\(\odot O\)，则此时点\(D\)的位置有三种：点\(D\)在\(\odot O\)外，点\(D\)在\(\odot O\)内，点\(D\)在\(\odot O\)上，

①当点\(D\)在\(\odot O\)外，如下图所示，记\(CD\)与\(\odot O\)相交于点\(E\)，

则由\(A\)，\(B\)，\(C\)，\(E\)四点共圆可知，\(\angle B+\angle CEA=180^{\circ}\)，

又由已知\(\angle A+\angle C=180^{\circ}\)，可得\(\angle B+\angle D=180^{\circ}\)，

则可知， \(\angle D=\angle CEA\)，

这与三角形的外角定理三角形的一个外角等于与它不相邻的两个内角的和。由此可得：三角形的外角大于任何一个与它不相邻的内角。\(\quad\)矛盾，故点\(D\)不在\(\odot O\)外；

②点\(D\)在\(\odot O\)内，如下图所示，记\(AD\)与\(\odot O\)相交于点\(E\)，

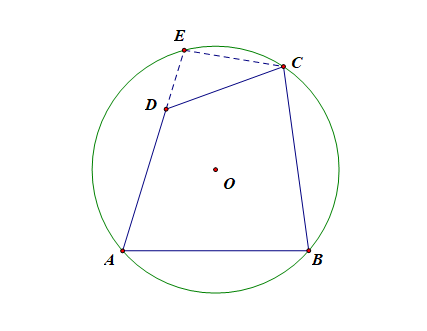
则由\(A\)，\(B\)，\(C\)，\(E\)四点共圆可知，\(\angle B+\angle CEA=180^{\circ}\)，

又由已知\(\angle A+\angle C=180^{\circ}\)，可得\(\angle B+\angle D=180^{\circ}\)，

则可知， \(\angle D=\angle CEA\)，

这与三角形的外角定理矛盾，故点\(D\)不在\(\odot O\)内；

综上所示，只能是点\(D\)在\(\odot O\)上，故\(A\)，\(B\)，\(C\)，\(D\)四点共圆；

判定定理的推论：

如果四边形的一个外角等于它的内角的对角，那么这个四边形的四个顶点共圆；

性质定理：

①圆内接四边形内角互补；

②圆内接四边形的外角等于它的内角的对角。

• 10、 弦切角定理

与圆相切的直线，同圆内与圆相交的弦相交所形成的夹角叫做弦切角。如图中\(\angle ABD\);

弦切角的度数等于它所夹的弧所对的圆心角度数的一半，等于它所夹的弧所对的圆周角度数。 即\(\angle ABD=\angle BCD\)

证明：\(\angle ABD+\angle OBD=90^{\circ}\)，\(\angle BOD=2\angle BCD\)，

又由于\(CD\)为直径，故\(\angle CBD=90^{\circ}\)，又由于\(OB=OD\)，则\(\angle OBD=\angle ODB\)

则\(\angle BCD+\angle OBD=90^{\circ}\)，

又由于\(AB\)为\(\odot O\)的切线，故\(\angle ABO=90^{\circ}\)

而\(\angle ABO=\angle ABD+\angle OBD=90^{\circ}\)，

故\(\angle ABD=\angle BCD\)；

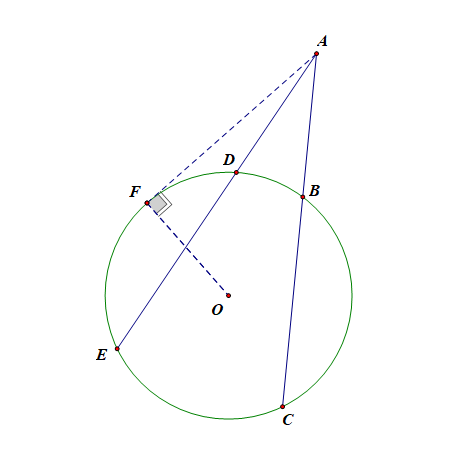
• 11、切割线定理

切割线定理：是指从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

一般用于求直线段长度。也是圆幂定理圆幂定理是一个总结性的定理，是对相交弦定理、切割线定理及割线定理（切割线定理推论）以及它们推论的统一与归纳。\(\quad\)之一。

即：\(AB^2=AD\cdot AC\)；

证明：由于\(\angle A=\angle A\)，\(\angle ABD=\angle BCA\)；

故\(\triangle ABD\sim \triangle ACB\)，故\(\cfrac{AB}{AC}=\cfrac{AD}{AB}\)，

整理得到，\(AB^2=AD\cdot AC\)；

切割线定理推论[也叫割线定理]:从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等。

• 12、三角形外角定理

外角定理:三角形的一个外角等于不相邻的两个内角和。

三角形内角和定理:三角形的三个内角和为180度。

多边形的外角和定理:多边形的外角和都等于360度。

拓展:在三角形中，已知其中两个角的度数，根据三角形内角和定理，则能求出第三个角的度数。

三角形的外角平分线定理:三角形的外角平分线外分对边所成的两条线段和相邻两边对应成比例。

• 13、三角形重心坐标公式

三角形\(\triangle ABC\)的重心\(M\)的坐标公式：若三角形的三个顶点坐标分别为\(A(x_1，y_1)\)，\(B(x_2，y_2)\)，\(C(x_3，y_3)\)，则其重心\(M(x_0，y_0)\)满足\(x_0=\cfrac{x_1+x_2+x_3}{3}\)，\(y_0=\cfrac{y_1+y_2+y_3}{3}\)。

三角形重心的性质的证明：

已知\(\triangle ABC\)的重心为\(G\)，\(D\)，\(E\)分别为边\(AC\)，\(BC\)的中点，求证：\(DG=\cfrac{1}{2}BG\)；

证明：连结\(DE\)，则可知\(DE\)为三角形的边\(AB\)的中位线，则有\(DE//AB\)，且\(DE=\cfrac{1}{2}AB\)，

则可知\(\triangle DEG\sim \triangle BAG\)，则有\(\cfrac{DG}{BG}=\cfrac{DE}{BA}=\cfrac{1}{2}\)，

即\(DG=\cfrac{1}{2}BG\)；同理可证，\(EG=\cfrac{1}{2}AG\)；